2004年结业于湖北轿车工业学院，结业后曾在国内轿车企业上任超越8年时刻，参加过轿车变速器研制、匹配、售后技术上的支撑等首要岗位。

　　行星齿轮传动的功率是点评其传动功能好坏的重要目标之一。关于不同传动类型的行星齿轮传动，其功率值的巨细也是不相同的。关于同一类型的行星齿轮传动，其功率值也或许随传动比ip的改变而改变。在同一类型的行星齿轮传动中，输入件、输出件不一起，其功率值也不相同。并且，行星齿轮传动功率改变规模很大，其值可高达0.98，低的可接近于零；乃至 0,即可自锁。

　　欲求得行星齿轮的传动功率值，首先应剖析和了解它的传动丢失。在行星齿轮传动中，其首要的功率丢失为如下三种。

　　（1）啮合齿轮副中的冲突丢失（简称啮合丢失），其相应的功率为。它是由于轮齿的齿廓滑动而引起的冲突丢失；值可以终究靠核算办法求得。

　　（2）轴承中的冲突丢失，其相应的功率为。由于各齿轮大都是安装在转轴上的，而这些转轴一般是借助于轴承支撑的。轴承丢失虽然也可以用核算的办法求得，但核算的差错比较大；特别是关于滑动轴承的冲突丢失的核算差错更大。

　　（3）液力丢失，其相应的功率为。它是由于光滑油的搅动和飞溅而引起的功率丢失。至今还没有针对行星齿轮传动可运用的核算公式。一般，在低速的简略齿轮传动（即定轴齿轮传动）中，其液力丢失与啮合丢失相比较要小得多。可是，关于行星齿轮传动，假如各齿轮均在油池中作业，其液力丢失就要比简略齿轮传动中的液力丢失大得多。尤其是当转臂x的转速比较大时，行星轮要在很短时刻内把光滑油从内齿轮b（或e轮）的齿根挤出，需求战胜的液体阻力很大。因而，在高速行星齿轮传动中应力求防止选用油池光滑。

　　在此应该指出的是：由于行星齿轮传动中存在着行星运动，故行星齿轮传动的功率与定轴齿轮传动的功率是不相同的，但在它们的功率核算办法上又有相同之处。一般那，行星齿轮传动的功率可由其转化组织（即其转臂x固定）所得到的功率（或用丢失系数）标明，即或标明。

　　在此还应指出，关于功率的写法与行星齿轮传动的传动比的写法相相似，和的上角标标明固定构件，两个下角标别离标明输入件和输出件。例如，2Z-X（A）型行星齿轮传动，当中心轮a输入，转臂x输出和内齿轮b固守时，其传动功率可标明为。而在转臂x固定的转化组织中，可用功率或丢失系数标明，其下角标可以省掉。

　　若疏忽行星齿轮传动中轴承的冲突丢失（因大都选用滚动轴承，故该冲突丢失很小），行星齿轮传动的啮合功率为

　　在行星齿轮窜动中，各构件之间的运动联系和作用力是必定的，故其各啮合副的冲突丢失功率PT应该为定植。

　　由于其转化组织各啮合齿轮副上的作用力与行星齿轮传动中的作用力是相同的。并且，在行星齿轮传动变为转化组织后，各构件之间的相对运动速度是不变的。所以，行星齿轮传动的冲突丢失功率PT应该与转化组织中的冲突丢失功率持平，即

　　现在，核算行星齿轮传动功率的办法许多，在规划核算中，较常用的行星齿轮传动功率的核算办法有下列三种：啮合功率法；力偏移法；传动比法（М.А.Крейнес克莱依涅斯法）。其间啮合功率法是使用比较遍及的办法。因而，本章侧重评论啮合功率法。所谓啮合功率法是使用啮合功率的概念来确认行星齿轮传动功率的一种办法。该办法是依据在行星齿轮传动与其转化组织中的冲突功率丢失持平的假定，即。经过转化组织的冲突功率丢失的联系式，再将行星齿轮传动的传动功率与其转化组织的传动功率联系起来，最终可求得行星齿轮传动功率的核算公式。

　　在行星齿轮传动中，因输入件的转速n1的方向与输入件的转矩T1的方向相同，故其传递功率为输入功率；输出件转速n2的方向与输出件的转矩T2的方向相反，其功率为输出功率。假如功率P=Tn中的转速n是相对某一构件而取的，则在功率符号P的右上角应注出该相对构件的代号。例如，构件a的转速是相对构件c而取的，则记为

　　在此，将称为啮合功率，其方向是有转化组织的输入件流向输出件。是标明在转化组织中所传递的功率，但并非实践存在的功率。它仅仅具有功率量纲，而不是能量的概念；值或许超越行星齿轮传动输入功率的许多倍。严格说来，由于与行星齿轮传动的实践功率P的概念不相同，故不能称为功率；可是，它却与功率P的量纲是相同的。因而，为了研讨行星齿轮传动的传动功率而借用了一个相当于功率的术语，且称之为啮合功率。啮合功率标志着在行星齿轮传动中的冲突丢失。啮合功率越大，则行星齿轮的传动功率越低。

　　用符号标明齿轮传动的啮合功率与传动功率（由肯定转速n得到的，而转速n是相关于固定构件的）之比值，且称为行星齿轮的啮合功率系数（或称相对功率系数）。例如，关于行星齿轮传动的中心轮a，则其捏合功率系数为

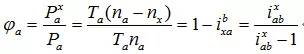
　　由上式可知，关于ix0的2Z-X型行星齿轮传动负号组织，则可得1，这标明它们的啮合功率小于传递的功率；因而，其冲突丢失小于转臂固守时的准行星传动的冲突丢失。当传动比趋近于1时，则值趋于无穷大。这标明该行星齿轮传动的冲突丢失比转臂固守时的准行星传动的冲突丢失大许多。关于ix0的2Z-X型行星齿轮传动正号组织，则得1，这标明它们的啮合功率大于所传递的功率；因而，其冲突丢失较大，故它们的传动功率较低。

　　别的，由于相对转速或许为正，也或许为负；据公式（1-6）可剖分出如下两点。

　　（1）啮合功率或许为正，也或许为负。当0时，构件a为转化组织的输入件，为转化组织的输入功率；当0时，构件a为转化组织的输出件，为转化组织的输出功率。

　　（2）啮合功率系数或许为正，也或许为负。当0时，啮合功率与所传递的功率的符号相同，这说明构件a在行星传动中与其转化组织中的输入或输出位置是相同的；当0时，与的符号相反，这说明构件a在行星传动中与其转化组织中的输入、输出位置是不相同的。

　　由此可见，在转化组织中啮合功率的活动方向与其对应的行星传动中传递功率P的活动方向也不必定相同。而在啮合功率的活动过程中相同存在着冲突功率丢失。

　　如前所述，由于行星齿轮传动与其转化组织中各构件间的相对转速、齿廓间的啮合作用力和冲突系数都是完全相同的，故行星齿轮传动与其转化组织的冲突功率丢失的巨细应根本持平，即。人们称此“定论”为啮合功率法原理。再依据原理，能愈加进一步推导与啮合功率的联系式。然后，依据啮合功率的不相同的状况，便可以别离求得其转化组织的传动功率。最终依据啮合功率系数的不相同的状况，便可以推导出行星齿轮传动的功率核算公式。

　　选用啮合功率以树立功率的核算公式是经过啮合功率流向的断定来进行的。首先应清晰行星齿轮传动中各构件输入、输出联系，再找出构件在行星齿轮传动中的实践功率与其在转化组织中的啮合功率之间的联系；最终就可以断定各构件在组织中的啮合功率的正负，即0或0，然后可知道构件在转化组织中为输入件，或输出件。由于，啮合功率总是由转化组织中的输入件流向输出件。所以，在找出输入件和输出件后，就可以正确地断定啮合功率的流向。

　　例如， 2Z-X（A）型行星齿轮传动中，内齿轮b固定，中心轮a输入，转臂x输出。由此可知，中心轮a在行星齿轮传动中的实践功率为正，即0。由于该行星齿轮传动是2Z-X型中的负号组织，即0，再依据公式（1-6）可得其啮合功

　　由于，0，所以，可得啮合功率为正，即0。这样就标明，中心轮a在行星齿轮传动中是输入件，在其转化组织中它仍然是输入件。则由此可断定：啮合功率是由中心轮a流向内齿轮b。

　　在2Z-X（A）型行星齿轮传动中，假如内齿轮b固定，中心轮a输出，转臂x输入。由此可知，中心轮a在行星齿轮传动中的实践功率为负，即0。因该行星齿轮传动仍是2Z-X（A）型负号组织，即0，此刻，0，依据公式（1-6）可得其啮合功率系数

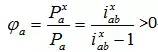
　　现已知0，则可得啮合功率为负，即0。这样就标明，中心轮a在行星齿轮传动中是输出件，在其转化组织中它仍是输出件。则由此可以断定：此刻啮合功率是由内齿轮b流向中心轮a。

　　由上述可知，关于2Z-X（A）型行星齿轮传动，当内齿轮b固守时，由于该行星齿轮传动为负号组织，即有0，则得其啮合功率系数0。所以，在行星齿轮传动和转化组织中，中心轮a的输入、输出的位置不变，即中心轮a在行星齿轮传动中是输入件或输出件，在其转化组织中它仍然是输入件或输出件。